解读Denoising Diffusion Probabilistic Models
一、DDPM在做什么
如果你想做一个文生图模型,给一段文字再随便给一张图(比如噪声),该模型就能帮你产出符合文字描述的逼真图片。文字描述就像一个指引(guidance),帮助模型去产生更符合语义信息的图片。但语义学习是复杂的,我们可以先退一步,让模型拥有产生逼真图片的能力。
比如,我们先给模型喂一堆cyberpunk风格的图片,让模型学会cyberpunk风格的分布信息,然后喂给模型一个随机噪音,就能让模型产生一张逼真的cyberpunk照片。或者给模型喂一堆人脸照片,让模型产生一张逼真的人脸。同样,我们也能选择给训练好的模型喂带点信息的图片,比如一张夹杂噪音的人脸,让模型帮我们去噪
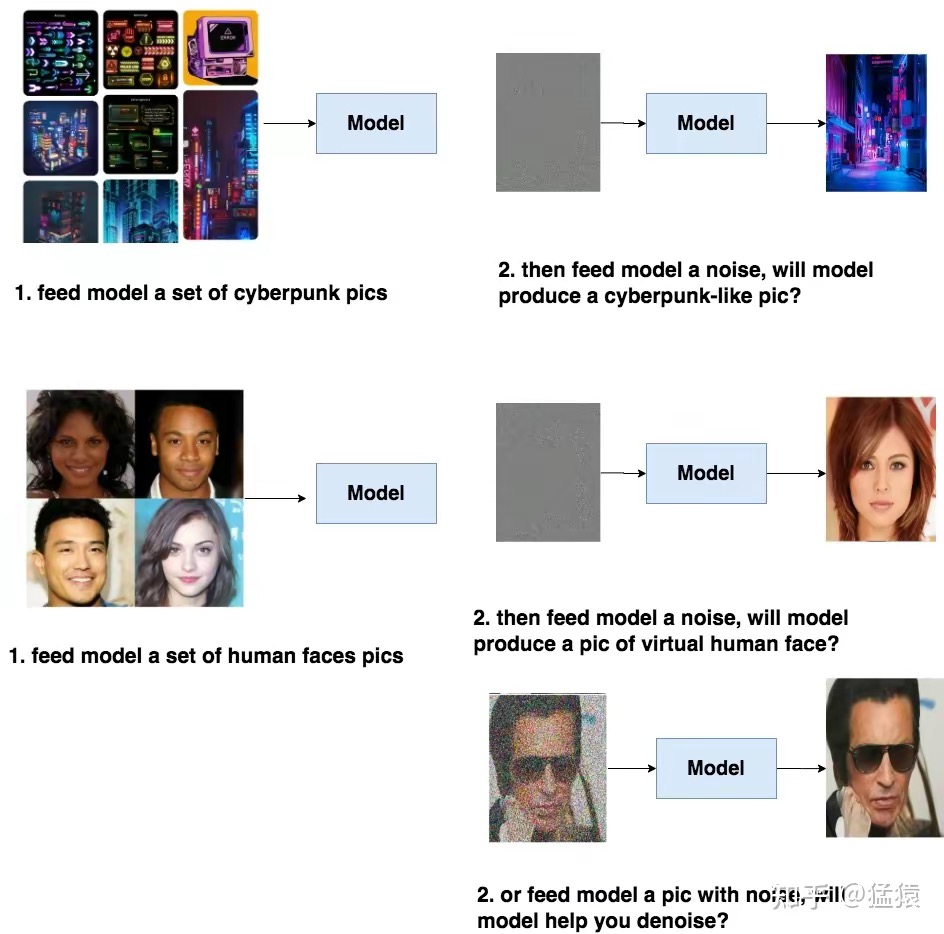
具备了产出逼真图片的能力,模型才可能在下一步去学习语义信息(guidance)。DDPM的本质作用,是学习训练数据的分布,产出尽可能符合训练数据分布的真实图片。所以,它也称为后续文生图类扩散模型框架的基石。
二、DDPM训练流程
总的来说,DDPM的训练过程分为两步:
- Diffsion Process(又称为Forward Process)
- Denoise Process(又被称为Reverse Process)
如何让模型学习训练数据的分布呢?
一个简单的想法是,使用一张干净的图,每一步(timestep)都往上加一点噪音,然后在每一步中,都让模型去找到加噪前图片的样子,即让模型学会去噪。这样训练完毕后,再给模型塞入一个纯噪声,它不就能一步步帮我还原出原始图片的分布了吗?
一步步加噪的过程,被称为Diffusion Process一步步去噪的过程,就被称为Denoise Process
2.1 Diffusion Process
Diffusion Process的命名收到热力学中分子扩散的启发:分子从高浓度区域扩散至低浓度区域,直至整个系统处于平衡。加噪过程也是同理,每次往图片上加一些噪声,直至图片变为一个纯噪声为止。整个过程如下:
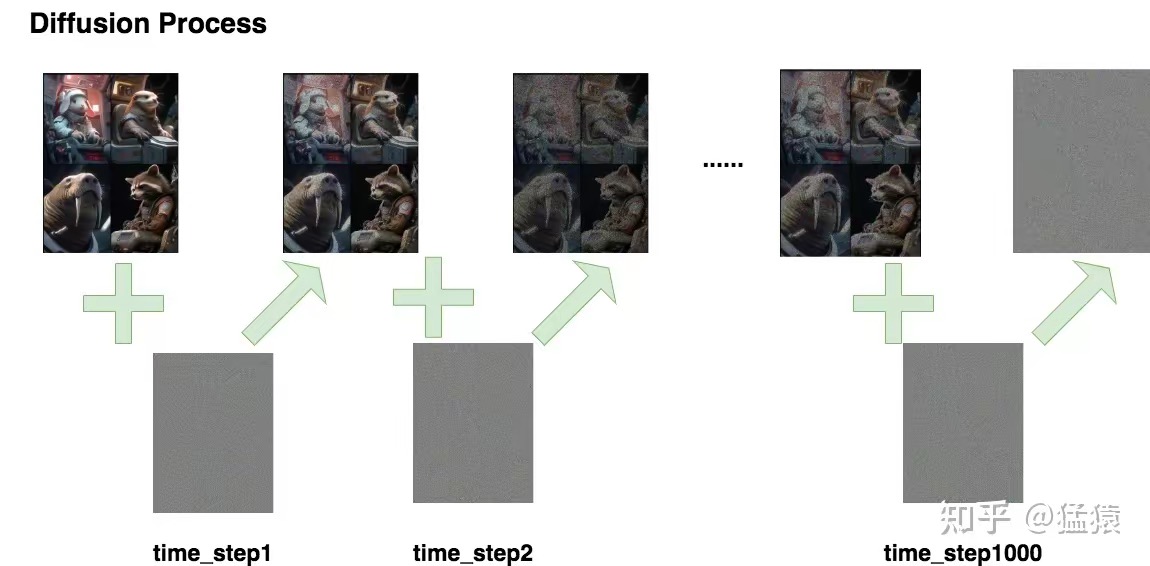
如图所示,我们进行了1000步加噪,每一步我们都往图片上加入一个高斯分布噪声,直到图片变为一个纯高斯分布的噪声。我们记:
- :总步数
- :每一步产生的图片。其中 为原始图片, 为纯高斯噪声
- :为每一步添加的高斯噪声
- : 在条件 下的概率分布。
那么根据以上流程图,我们有:
根据公式,为了知道 ,需要sample好多次噪声,感觉不太方便,能不能更简化一些呢
重参数
我们知道随着步数的增加,图片中原始信息含量越少,噪声越多,我们可以分别给原始图片和噪声一个权重来计算 :
- :一系列常数,类似于超参数,随着的增加越来越小
此时的计算可以设计成:。现在,我们只需要sample一次噪声,就可以直接从得到了。
再深入一些,并不是我们直接设定的超参数,而是根据其他参数推导而来的,这个“其他超参数”指:
- :一系列常数,是我们直接设定的超参数,随着T的增加越来越大
则和的关系可以表示为:
这样从原始加噪到加噪,再到加噪,使得转换成的过程,就被称为重参数(Reparameterization)
2.2 Denoise Process
Denoise Process的过程与Diffusion Process恰好相反:给定,让模型把它还原到,这里我们用来表示去噪过程。由于加噪过程只是按照设定好的超参数向前加噪,并不经过模型,而去噪过程是真正训练并使用模型的过程,所以我们用来表示去噪过程,表示模型参数。即:
:用来表示Diffusion Process
:用来表示Denoise Process
我们再来看看去噪模型做了什么事。如图所示,从第个timestep开始,模型的输入为与当前timestep 。模型中蕴含一个噪声预测器(UNet),该预测器会根据当前的输入预测出噪声,然后将图片减去预测出的噪声,就可以得到去噪后的图片。重复这个过程,直到还原出原始图片为止:
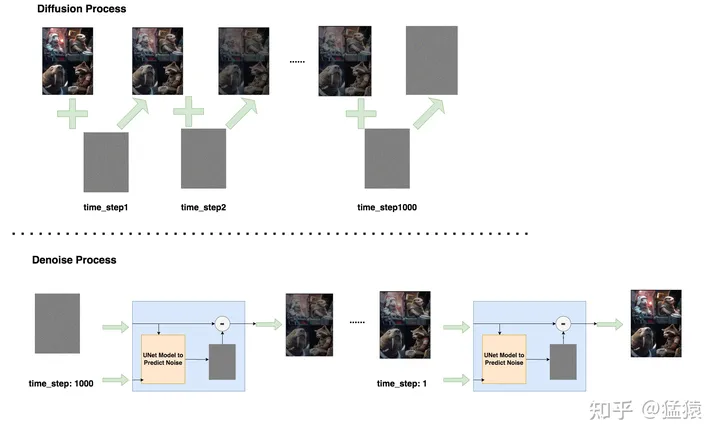
这里就有两个(至少)疑惑:
-
为什么我们的输入要包含timestep?
由于模型每一步去噪都是用的同一个模型,所以我们需要告诉模型现在进行的是哪一步去噪,因此我们要引入timestep。
-
为什么通过预测噪声的方式,就能让模型学得训练数据的分布,从而产生逼真的图片?
我们知道DDPM的优化目标是:**使得生成的图片尽可能符合训练数据分布。**基于这个目标我们记:
- :模型所产生的图片的(概率)分布。其中表示模型参数。
- :训练数据(也可理解为真实世界)图片的(概率)分布。其中data表示这是一个自然世界客观存在的分布,与模型无关。
则我们的优化目标如图:
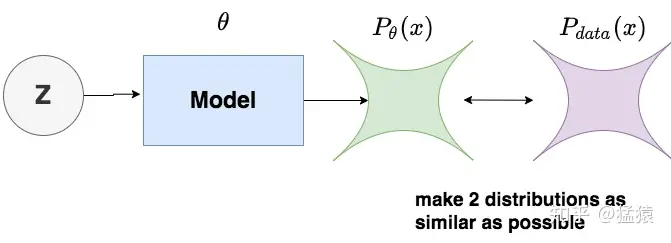
让和两个分布尽可能相似。而求两个分布的相似性,则可以想到**KL散度。**现在我们的目标函数就变为:。
我们利用KL散度的公式对目标函数做一些变换:

可以将优化目标变为求
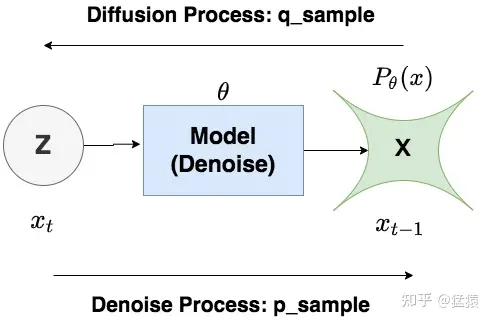
回顾:在Diffusion Process中,我们不过模型,随timestep的变化给图片加噪。在Denoise Process中,我们经过模型,对图片进行去噪。Diffusion过程中遵循的分布记为,Denoise过程中遵循的分布,记为。
现在我们可以继续拆解:

被称为Evidence Lower Bound(ELBO)。至此,我们将最大化拆解为最大化ELBO。
该式描述的是一个timestep下的优化目标,但我们的模型有个timestep,因此还需进一步扩展成链式表达的方式。这里,为了更符合我们对扩散模型的理解,我们不再使用变量,将其用来表示:
继续拆解:
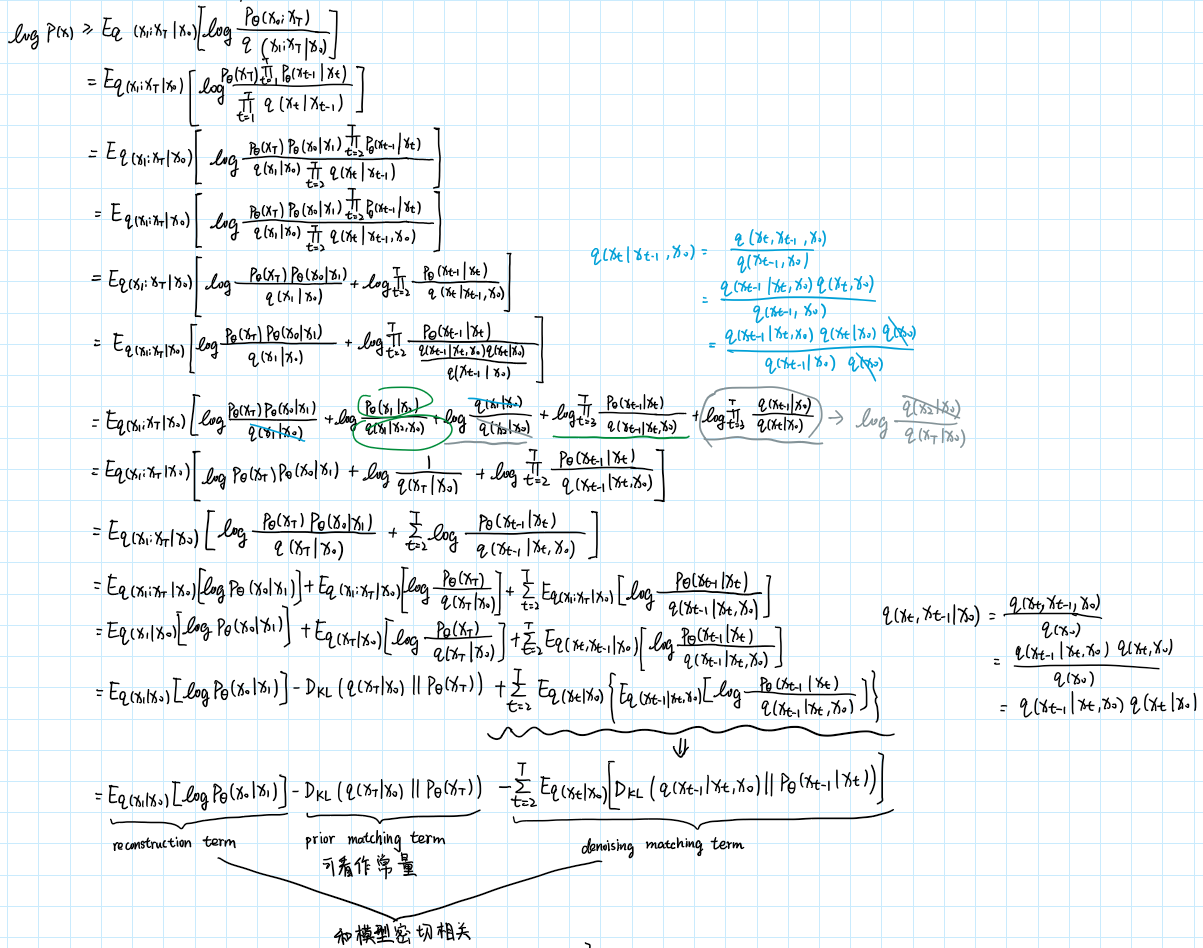
其中prior matching term可看作是常量,reconstruction term和denoising matching term则是和模型密切相关的两项。由于两者十分相似,接下来只需特别关注denoising matching term如何拆解即可。

接下来我们来看长什么样。同时,我们已经知道(最初假设)都服从高斯分布,根据高斯分布的性质,我们有:
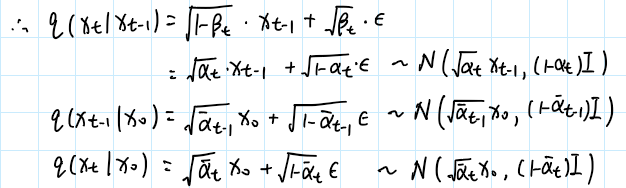
对于高斯分布,知道了均值和方差,我们就可以把它的概率密度函数写出来:

一顿推导后,我们将的分布写出来了,也就是我们当前优化目标中q的部分。现在我们再看部分,根据优化目标,我们需要让和的分布尽量接近:
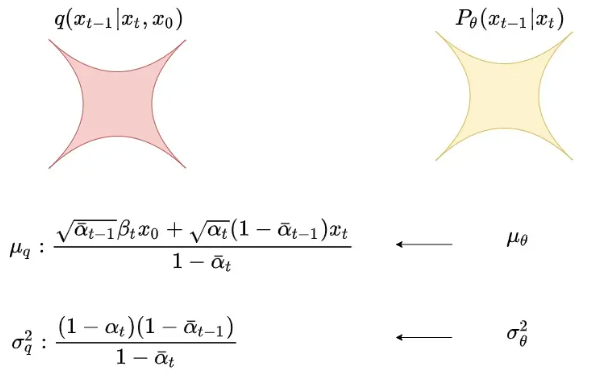
而让和的分布接近,等价于让。注意到其实是一个常量,只和我们设置的超参数有关。在DDPM中,为了简化优化过程,并且使训练更稳定,就假设也按此种方式固定下来。在DDPM中,只预测均值。
于是我们再对做改写,根据diffusion规则,将用表示:
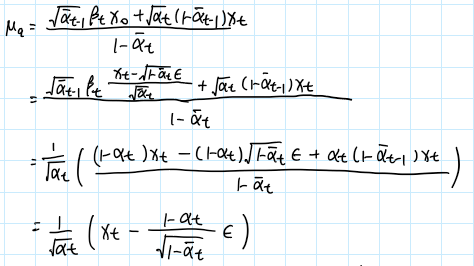
可以看出,上式的结果在diffusion过程中就已决定。所以对于,我只需让它在denoise过程中预测出,使得,然后令:
这样,我们就能使得和的分布一致。
也就是说,只要在denoise的过程中,让模型去预测噪声,就可以达到“让模型产生图片的分布”和“真实世界的图片分布”逼近的目的。
三、DDPM的Training与Sampling过程

在training过程中,我们只需要去预测噪声,就能在数学上使得模型学到的分布和真实的图片分布不断逼近。
- 从训练数据中,抽样出一条
- 随机抽样出一个timestep
- 随机抽样出一个噪声
- 计算:
- 计算梯度,更新模型,重复上述过程
而当我们使用模型去做sampling,即测试模型能生成什么样的图片时,我们可由
从推导,甚至还原出。
DDPM的核心运作方法已经讲完了,接下来我们看DDPM用于预测噪声的核心模型:UNet。
四、DDPM中的UNet架构
总的来说,UNet分为两个部分:
- Encoder
- Decoder
在Encoder部分中,UNet模型会逐步压缩图片的大小;在Decoder部分中,则会逐步还原图片的大小。同时在Encoder和Decoder间,还会使用“残差连接”,确保Decoder部分在推理和还原图片信息时,不会丢失掉之前步骤的信息。整体示意图如下,因为压缩再放大过程形似U字,因此被称为UNet:
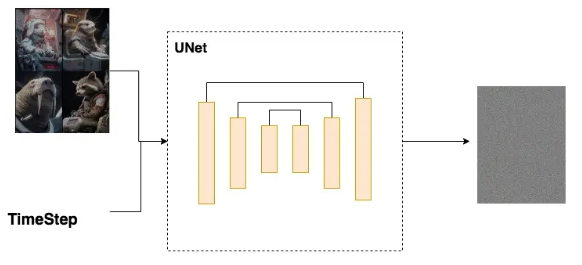
DDPM中的UNet是什么样子?我们假设输入一张32323大小的图片,看一下DDPM UNet运作的完整流程:
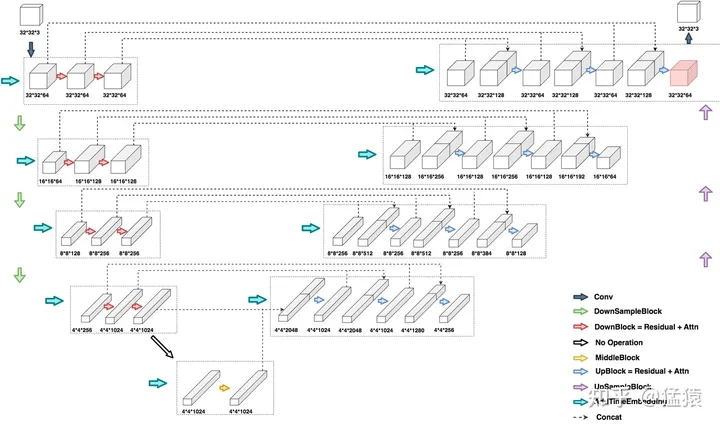
同层间只做channel上的变化,不同层间做图片的压缩处理。至于每一层channel怎么变,层间size如何调整,就取决于实际训练中对模型的设定了。Decoder层也是同理。
4.1 DownBlock和UpBlock
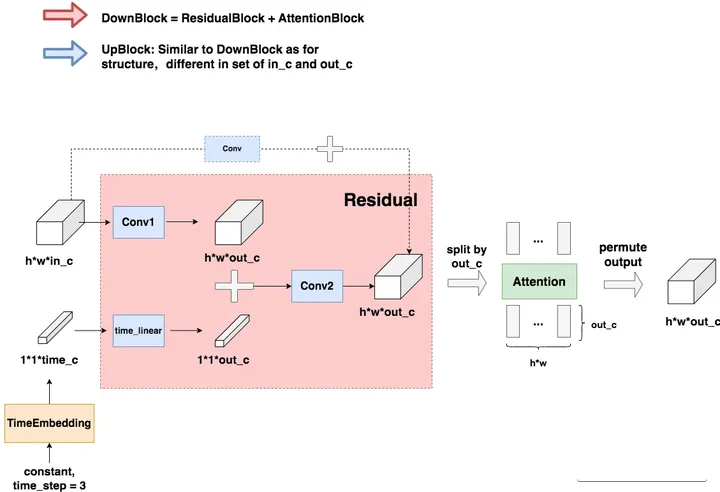
TimeEmbedding层采用和Transformer一致的三角函数位置编码,将常数转变为向量。Attention层则是沿着channel维度将图片拆分为token,做完attention后再重新组装成图片。
虚线部分即为“残差连接”(Residual Connection),而残差连接之上引入的虚线框Conv的意思是,如果in_c = out_c,则对in_c做一次卷积,使得其通道数等于out_c后,再相加;否则将直接相加
4.2 DownSample和UpSample
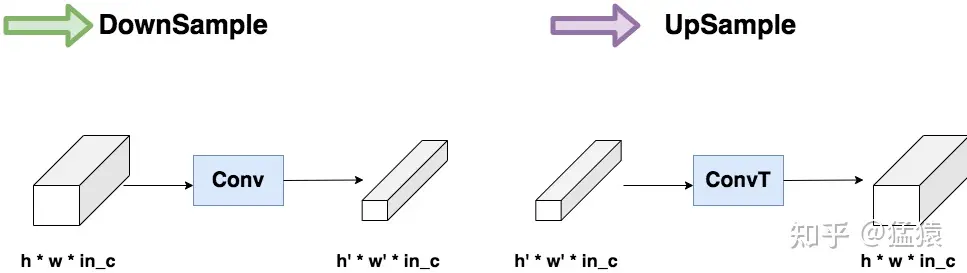
就是**压缩(Conv)和放大(ConvT)**图片的过程。
4.3 MiddleBlock
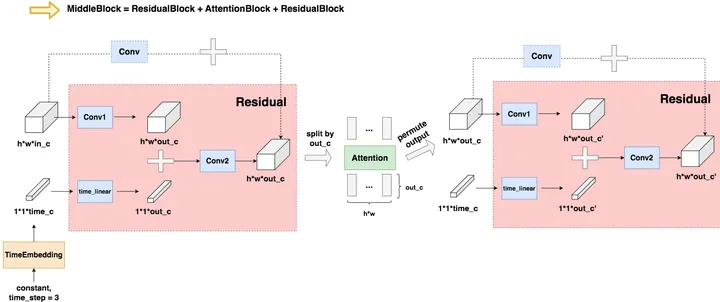
和DownBlock与UpBlock的过程相似,不再赘述。





